Fourier: Making Waves
|
Topics
- Waves
- Sines
- Cosines
Description
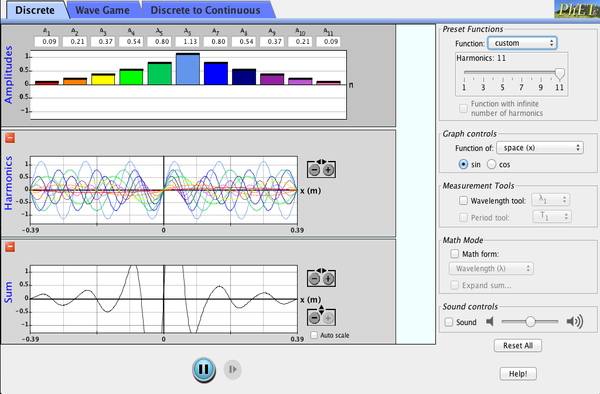
Learn how to make waves of all different shapes by adding up sines or cosines. Make waves in space and time and measure their wavelengths and periods. See how changing the amplitudes of different harmonics changes the waves. Compare different mathematical expressions for your waves.
Sample Learning Goals
- Explain qualitatively how sines and cosines add up to produce arbitrary periodic functions.
- Recognize that each Fourier component corresponds to a sinusoidal wave with a different wavelength or period.
- Mentally map simple functions between Fourier space and real space.
- Describe sounds in terms of sinusoidal waves.
- Describe the difference between waves in space and waves in time.
- Recognize that wavelength and period do not correspond to specific points on the graph but indicate the length/time between two consecutive troughs, peaks, or any other corresponding points.
- Become comfortable with various mathematical notations for writing Fourier transforms, and relate the mathematics to an intuitive picture of wave forms.
- Determine which aspect of a graph of a wave is described by each of the symbols lambda, T, k, omega, and n.
- Recognize that lambda & T and k & omega are analogous, but not the same.
- Translate an equation from summation notation to extended notation.
- Recognize that the width of a wave packet in position space is inversely related to the width of a wave packet in Fourier space.
- Explain how the Heisenberg Uncertainty principle results from the properties of waves.
- Recognize that the spacing between Fourier components is inversely related to the spacing between wave packets, and that a continuous distribution of fourier components leads to a single wave packet.
Version 3.06
Keywords
Teacher Tips
| Overview of sim controls, model simplifications, and insights into student thinking ( PDF ). |
Teacher-Submitted Activities
| Title |
|
|
Authors | Level | Type | Subject |
|---|---|---|---|---|---|---|
| Concept questions for Physics using PhET (Inquiry Based) |
|
|
Trish Loeblein | HS UG-Intro |
MC | Physics |
| Wave unit (Inquiry Based) |
|
|
Trish Loeblein | HS UG-Intro |
Lab Demo |
Physics |
| Wave clicker questions (Inquiry Based) |
|
|
Trish Loeblein | HS UG-Intro |
CQs | Physics |
| Waves: Superposition (Inquiry Based) |
|
|
Trish Loeblein | HS UG-Intro |
Lab CQs |
Mathematics Physics |
| Wave Representations (Inquiry Based) |
|
|
Trish Loeblein | UG-Intro HS |
Lab | Physics |
| Fourier Making Waves Game (Inquiry Based) |
|
|
Trish Loeblein | HS | Lab | Physics |
| Wave Modeling and Wave addition (Inquiry Based) |
|
|
Trish Loeblein | HS UG-Intro |
Lab | Physics |
| How do PhET simulations fit in my middle school program? |
|
Sarah Borenstein | MS | Other | Earth Science Biology Physics Chemistry |
|
| Alignment of PhET sims with NGSS |
|
Trish Loeblein | HS | Other | Physics Biology Earth Science Chemistry |
|
| Introduction to Fourier Analysis |
|
Sam McKagan, Kathy Perkins and Carl Wieman | UG-Adv UG-Intro |
HW | Physics Mathematics |
|
| MS and HS TEK to Sim Alignment | Elyse Zimmer | HS MS |
Other | Chemistry Biology Physics |
||
| Mapping of PhET and IBDP Physics | Jaya Ramchandani | HS | Other | Physics | ||
| Making use of the Sound Simulations | Don Cameron | HS | Lab | Physics |
| Design Team | Third-party Libraries | Thanks To |
|---|---|---|
|